Dropout Regularization
Dropout
- We reviewed the impact of dropout applied to features of size $( B \times C )$, where $( B )$ is the number of samples per batch (batch size) and $( C )$ is the number of channels (or features).
- The general formula: $( y = X \cdot m \cdot \text{scale} )$.
- Applying dropout to features of size $( B \times C )$ still results in an output of the same size.
How does the mask impact memory during training?
While the masks used in dropout regularization introduce some additional memory overhead during training, this impact is generally modest compared to the overall memory usage of the neural network model. The benefits of improved generalization and reduced overfitting often outweigh the minor increase in memory usage.
Mask Scaling
What does it mean?
Dropout involves a “mask” that determines which neurons to drop. This mask can be scaled by a certain factor. The scaling factor $( \frac{1}{1-p} )$ ensures that the expected value of the output during training remains the same as it would be without dropout.
Where can we apply masking and scaling?
There are two places where it can happen:
- During Training: More efficient to scale the mask once at the beginning.
- During Inference: Less efficient because the mask needs to be scaled every time you make a prediction.
Why do we turn off dropout regularization during inference?
Turning off dropout regularization during inference ensures stability, full utilization of the model’s capacity, efficiency, consistency with training expectations, and deterministic output.

Forward and Backward Passes
- During backpropagation, the chain rule is applied. Let’s denote the output of the layer before dropout as $( X )$ and the output after dropout as $( y )$. We have:
$$
y = X \cdot \left( \frac{m}{1-p} \right)
$$
where $( m )$ is the binary mask (0s and 1s). - To find the derivative of the loss $( L )$ with respect to $( X )$, we use the chain rule:
$$
\frac{dL}{dX} = \left( \frac{dL}{dy} \right) \cdot \left( \frac{dy}{dX} \right)
$$
where $( \frac{dy}{dX} = \frac{m}{1-p} )$. Therefore, the scaling factor in the dropout mask directly affects the gradient flowing back to the layer. - The derivative of the output $( y )$ with respect to the input $( X )$, $( \frac{dy}{dX} )$, is a matrix with the same shape as $( X )$, where each element is either 0 (if the corresponding element in the mask $( m )$ is 0) or $( \frac{1}{1-p} )$ (if the corresponding element in $( m )$ is 1).

Neural Network Training
Neural networks often seek the simplest solutions, which can be shallow or suboptimal. There are two primary approaches to improving inference accuracy:
- Training on a Large Amount of Data: While this can enhance performance, it has its limitations. There’s a point of diminishing returns where adding more data doesn’t yield significant improvements. Additionally, obtaining high-quality, labeled data can be both expensive and time-consuming.
- Using Dropout Regularization Methods: Dropout regularization introduces a challenge (stochasticity) into the learning process by randomly deactivating a portion of neurons. This prevents over-reliance on specific features and forces the neural network to adapt and find alternative pathways, leading to the discovery of deeper, more robust representations within the data.
Convolutional Neural Network (CNN)
- What it means: CNNs are designed to handle the spatial structure of images effectively.
- Feature Size: The size $( BHWC )$ describes the dimensions of feature maps within a CNN.
- B (Batch Size): Number of images processed simultaneously in a batch during training.
- H (Height) and W (Width): Spatial dimensions of the feature map.
- C (Channels): Number of feature maps at a given layer (e.g., 3 for RGB images).
- Feature Maps: Outputs of convolutional layers within a CNN, highlighting specific patterns or features within an image.
- Pattern Extraction: Feature maps extract patterns, starting with simple edges and corners in early layers, and becoming increasingly complex (textures, object parts) in deeper layers.
Other Types of Dropouts
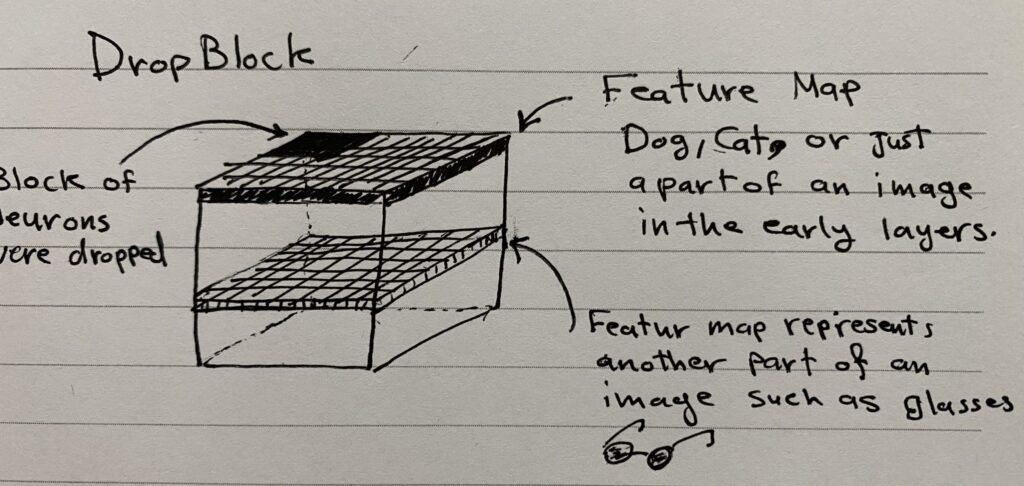
Dropblock
A regularization technique where contiguous regions (blocks) of neurons/elements are dropped out within a feature map. This method is more effective than traditional dropout for CNNs because it considers the spatial structure of images, making it harder for the model to infer the missing neurons.
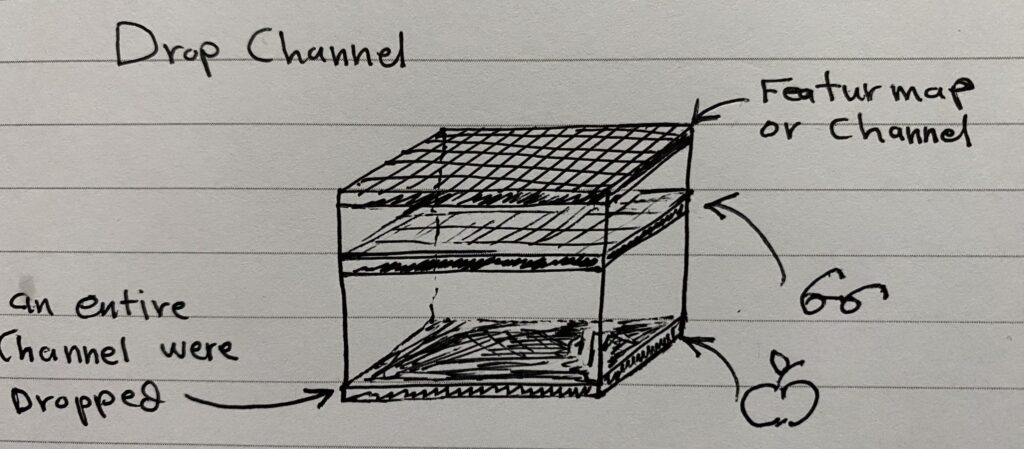
Drop Channel
Entire channels (like color channels in an image) are dropped instead of individual neurons. This technique randomly removes entire channels from feature maps during training, which is useful in CNNs dealing with multi-channel inputs (e.g., RGB images).
Drop Layer
Involves dropping out entire layers within a deep neural network. Dropping entire layers is less common, but it can be effective with architectures like ResNet that use residual connections, where $( y = x + d(f(x)) )$. Residual connections allow the model to learn an identity mapping if needed, facilitating the training of very deep networks.

